Using Gappa from other tools

Why and Gappa

The Why software verification platform can be used to translate code annotated with pre- and postconditions into proof obligations suitable for Gappa.

By installing Frama-C first and then Why (in order to build the Jessie plugin), one gets a tool for directly certifying C programs with Gappa.

Example: floating-point square root

The example below demonstrates the usage of these tools. The C file defines a sqrt function that computes the square root with a relative accuracy of \(2^{-43}\) for an input x between 0.5 and 2.

/*@
 requires 0.5 <= x <= 2;
 ensures \abs(\result - 1/\sqrt(x)) <= 0x1p-6 * \abs(1/\sqrt(x));
*/
double sqrt_init(double x);

/*@
 lemma quadratic_newton: \forall real x, t; x > 0 ==>
   \let err = (t - 1 / \sqrt(x)) / (1 / \sqrt(x));
   (0.5 * t * (3 - t * t * x) - 1 / \sqrt(x)) / (1 / \sqrt(x)) ==
   - (1.5 + 0.5 * err) * (err * err);
*/

/*@
 requires 0.5 <= x <= 2;
 ensures \abs(\result - \sqrt(x)) <= 0x1p-43 * \abs(\sqrt(x));
*/
double sqrt(double x)
{
  int i;
  double t, u;
  t = sqrt_init(x);

  /*@ loop pragma UNROLL 4;
    @ loop invariant 0 <= i <= 3; */
  for (i = 0; i <= 2; ++i) {
    u = 0.5 * t * (3 - t * t * x);
    //@ assert \abs(u - 0.5 * t * (3 - t * t * x)) <= 1;
    /*@ assert \let err = (t - 1 / \sqrt(x)) / (1 / \sqrt(x));
          (0.5 * t * (3 - t * t * x) - 1 / \sqrt(x)) / (1 / \sqrt(x)) ==
          - (1.5 + 0.5 * err) * (err * err); */
    //@ assert \abs(u - 1 / \sqrt(x)) <= 0x1p-10 * \abs(1 / \sqrt(x));
    t = u;
  }

  //@ assert x * (1 / \sqrt(x)) == \sqrt(x);
  return x * t;
}

The code starts by calling the sqrt_init function. It returns an approximation of \(x^{-1/2}\) with a relative accuracy of \(2^{-6}\). Only the specification of this auxiliary function is given. (Preconditions are introduced by the requires keyword, while postconditions are introduced by ensures.) Its implementation could use small tables for instance. Note that bounds on relative errors are expressed as \(|\mathit{approx} - \mathit{exact}| \le \mathit{error} \times |\mathit{exact}|\) in this setting.

The sqrt function then performs three Newton iterations in order to obtain an improved approximation of the reciprocal square root of x. Since Gappa only handles straight-line programs, a pragma annotation instructs Frama-C to completely unroll the loop before passing it to Jessie. Finally, once the reciprocal square root has been computed, it is multiplied by x to obtain the square root.

Passing hints through annotations

The assert annotations cause Frama-C/Jessie to generate additional proof obligations. These facts are then available to the following proof obligations as hypotheses. In this example, the actual content of the assertions does not matter from a certification point of view, they are only used as a way to pass information to Gappa. Indeed, as explained in ref:example-fixed, Gappa needs to know about Newton’s relation and which expressions are approximations of what. So, if the program were to be directly expressed in Gappa syntax, the three loop assertions would instead have been written as follows.

rsqrt = 1 / sqrt(x);
err = (t - rsqrt) / rsqrt;
{ ... }
u ~ 0.5 * t * (3 - t * t * x);
(0.5 * t * (3 - t * t * x) - rsqrt) / rsqrt -> - (1.5 + 0.5 * err) * (err * err);
u ~ rsqrt;

When writing these assertions for guiding Gappa, one just as to make sure that they are easily provable; their actual accuracy is not relevant. For instance, if the relative distance between u and \(1 / \sqrt{x}\) had been \(2^{-1}\) instead of \(2^{-10}\), Gappa would still have succeeded.

Execution results

Passing the program above to the Frama-C/Jessie tool produces the following console output…

$ frama-c -jessie a.c
[kernel] preprocessing with "gcc -C -E -I.  -dD a.c"
[jessie] Starting Jessie translation
[kernel] No code for function sqrt_init, default assigns generated
[jessie] Producing Jessie files in subdir a.jessie
[jessie] File a.jessie/a.jc written.
[jessie] File a.jessie/a.cloc written.
[jessie] Calling Jessie tool in subdir a.jessie
Generating Why function sqrt
[jessie] Calling VCs generator.
gwhy-bin [...] why/a.why
Computation of VCs...
Computation of VCs done.
Reading GWhy configuration...
Loading .gwhyrc config file
GWhy configuration loaded...
Creating GWhy Tree view...

…and displays the following user interface.

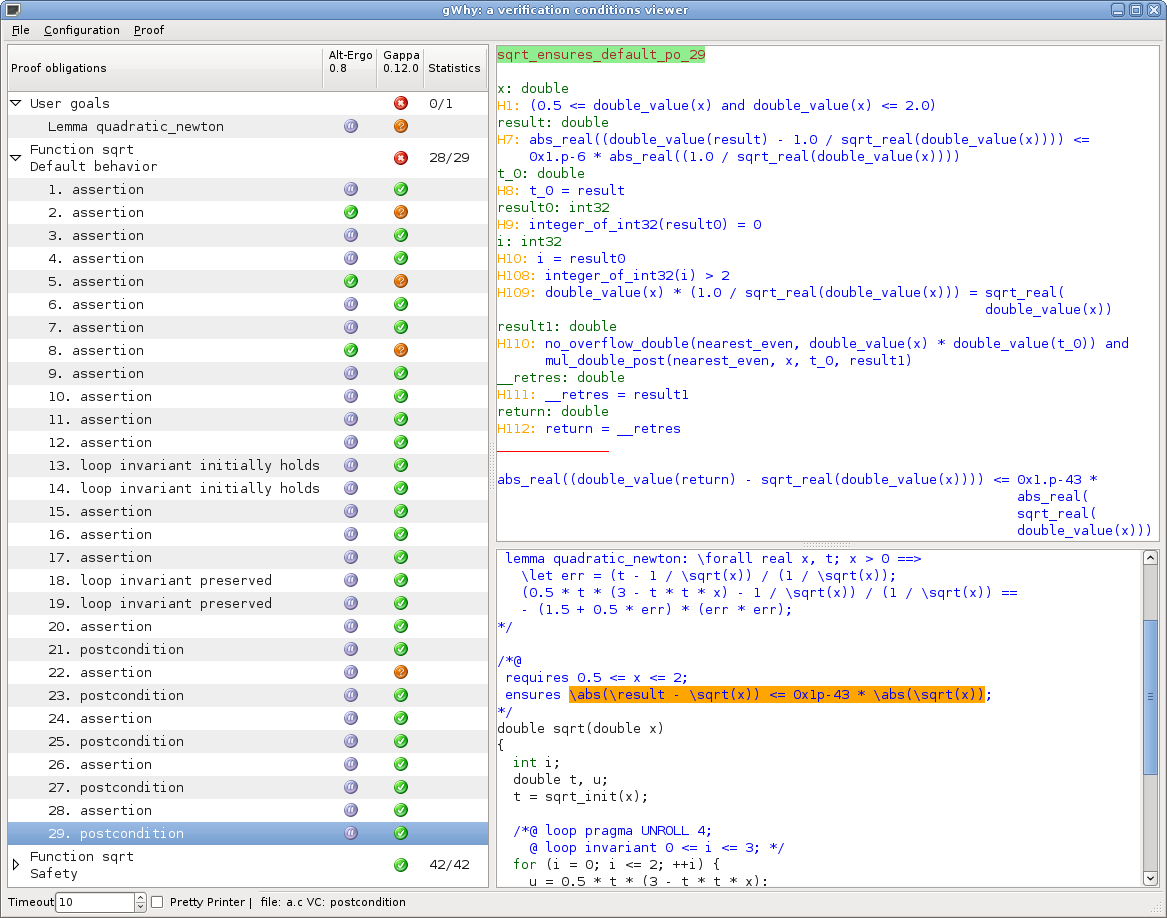
On the left of the window are the proof obligations. Once all of them are proved, the code is guaranteed to match its specification. Green marks flag proof obligations that were automatically proved. Selected proof obligations are displayed on the right; here it is the postcondition of the sqrt function.

Gappa is not able to prove Newton’s relation nor does it know that \(x \times \sqrt{x}^{-1} = \sqrt{x}\) holds. These assertions are therefore left unproved. Due to loop unrolling, Newton’s relation appears three times. To factor these occurrences, a lemma describing the relation has been added to the C code. The Alt-Ergo prover is used to check that the three occurrences indeed match this lemma.

In the end, we have 72 proof obligations and only two of them are left unproved by the combination of Gappa and Alt-Ergo. They are mathematical identities on real-valued expressions, so they could easily be checked with an interactive proof assistant or a computer algebra system. (And they should be, at least for Newton’s relation, because of its error-prone expression.)

Coq and Gappa

The Gappa Coq Library adds a gappa tactic to the Coq Proof Assistant. This tactic invokes Gappa to solve properties about floating-point or fixed-point arithmetic. It can also solve simple inequalities over real numbers.

The tactic is provided by the Gappa_tactic module. It expects to find a Gappa executable (called gappa) in the user program path.

From Coq Require Import Reals.
From Flocq Require Import Core.
From Gappa Require Import Gappa_tactic.
Open Scope R_scope.

Goal
  forall x y : R,
  3/4 <= x <= 3 ->
  0 <= sqrt x <= 1775 * powerRZ 2 (-10).
Proof.
  gappa.
Qed.

The tactic recognizes fully-applied rounding_fixed and rounding_float functions as rounding operators.

The script below proves that the difference between two double precision floating-point numbers in \([\frac{52}{16}, \frac{53}{16}]\) and \([\frac{22}{16}, \frac{30}{16}]\) is exactly representable as a double-precision floating-point number. (Rounding direction does not matter for this example; it has been arbitrarily chosen as rounding toward zero.)

Definition rnd := rounding_float rndZR 53 (-1074).

Goal
  forall a_ b_ a b : R,
  a = rnd a_ ->
  b = rnd b_ ->
  52 / 16 <= a <= 53 / 16 ->
  22 / 16 <= b <= 30 / 16 ->
  rnd (a - b) = (a - b).
Proof.
  unfold rnd; gappa.
Qed.

The tactic handles goals and hypotheses that are either equalities of real numbers, \(e_1 = e_2\), or pairs of inequalities on real numbers, \(b_1 \le e \le b_2\), or inequalities expressing relative errors, \(|e_1 - e_2| \le b \cdot |e_2|\). For inequalities, the b bounds have to be explicit dyadic numbers. The tactic also recognizes properties written as \(|e| \le b\) as syntactic sugar for \(0 \le |e| \le b\).

The tactic is built on Flocq’s formalism and uses the same rounding operators and formats. The previous goal could therefore have been written in a slightly more natural way.

Definition format :=
  generic_format radix2 (FLT_exp (-1074) 53).

Goal
  forall a b : R,
  format a -> format b ->
  52 / 16 <= a <= 53 / 16 ->
  22 / 16 <= b <= 30 / 16 ->
  format (a - b).
Proof.
  unfold format; gappa.
Qed.